Homework Assignment 4
1. HDR Imaging
Use dcraw to convert the RAW .NEF images into linear 16-bit .TIFF images
Ubuntu 20.04.2 LTS command line 환경으로 dcraw를 사용하였음. 사용한 flags에 대한 정보는 다음과 같음.
-i -v shows metadata.
-v Print verbose messages, not just warnings and errors.
-q 3 Use Adaptive Homogeneity-Directed (AHD) interpolation.
-o [0-6]
Select the output colorspace when the -p option is not used:
0 Raw color (unique to each camera)
1 sRGB D65 (default)
2 Adobe RGB (1998) D65
3 Wide Gamut RGB D65
4 Kodak ProPhoto RGB D65
5 XYZ
6 ACES
-w Use the white balance specified by the camera. If this is not found, print a
warning and use another method.
-T Write TIFF with metadata instead of PGM/PPM/PAM.
결과적으로 사용한 flags는 -v -w -T -o 1 -q 3 임.
Linearize rendered images
Image sampling
본 프로젝트에서는 16장의 고해상도 이미지를 사용하기 때문에 매우 많은 연산량을 요구함. 따라서 모든 픽셀을 사용하여 Response curve를 구하지 않고 sampling된 이미지를 사용함. 사용되는 픽셀 N은 다음과 같은 조건을 만족해야함.
따라서 본 프로젝트에서는 N = 100 을 사용할 것임. matlab의 imresize 를 사용하여 subsampling을 진행하였음.
R = imresize(images(:,:,1, p), [10, 10]);Response curve
Response curve를 구하기 위하여 gsolve 함수를 정의하였음. 이전 과제와 마찬가지로 SVD를 통하여 g 를 구하였음.
n = 256;
A = zeros(size(Z, 1)*size(Z,2)+n+1, n+size(Z, 1));
b = zeros(size(A, 1), 1); % exposure value
k = 1;
for i = 1:size(Z, 1)
for j = 1:size(Z, 2)
wij = w(Z(i, j)+1);
A(k, Z(i, j)+1) = wij;
A(k, n+i) = -wij;
b(k, 1) = B(j) * wij;
k = k+1;
end
end
A(k, 129) = 1;
k = k+1;
for i = 1:n-2
A(k, i) = l*w(i+1);
A(k, i+1) = -2*l*w(i+1);
A(k, i+2) = l*w(i+1);
k = k+1;
end
x = A\b;
g = x(1:n, 1); % the log exposure corresponding to pixel value z
IE = x(n+1:size(x,1), 1); % the log film irradiance at pixel location i이때 사용되는 weight function w 의 경우, 이미지 Z의 range가 0-255로 가정하고 사용의 편이를 위해서 다음과 같이 linear weighting function과 tent weighting function을 정의하였음.
for i = 1:256
w(i) = 1;
end
for i = 1:256
if i <= 256/2
w(i) = i-1;
else
w(i) = 256 - i;
end
endPlot the function g
tent weighting function을 통해서 구한 g를 plot한 결과는 다음과 같음.
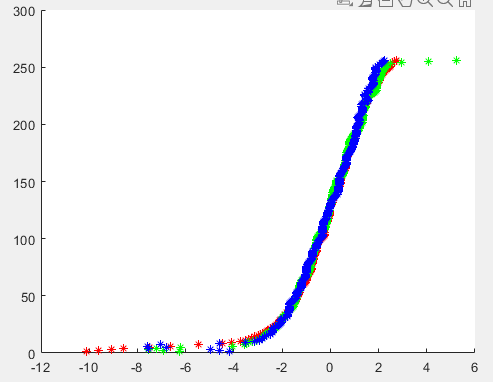
uniform weighting function을 통해서 구한 g를 plot한 결과는 다음과 같음.
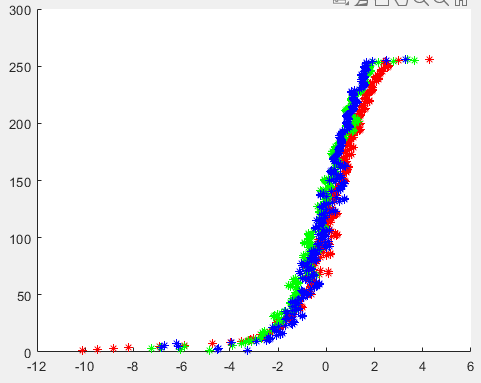
uniform weighting function보다 tent weighting function을 사용하였을때 결과가 더 좋은 것을 확인할 수 있다.
Convert the non-linear images I into linear ones
마지막으로 다음과 같이 non-linear image를 linear image로 변환하는 과정을 거침
linear_images(w, h, 1, p) = exp(gr(images(w, h, 1, p)+1));Merge exposure stack into HDR image
Weighting function
본 프로젝트에서는 image의 range를 [0, 255]로 가정하고 weight function을 구현하였음
먼저 uniform weighting function의 경우 모든 경우에 대해서 weight를 1로 동일하게 두었음
function w = weighting_uniform(~)
w = 1;
endTent weighting function의 경우 0-255 범위를 벗어나는 경우에 대해서는 0으로 처리하였음
function w = weighting_tent(z)
Zmin = 0;
Zmax = 255;
if z <= 255*0.5
w = z-Zmin;
if w < 0
w = 0;
end
else
w = Zmax-z;
if w < 0
w = 0;
end
end
endLinear merging
linear merging의 경우 앞서 구한 linear image를 사용하여 값을 구하였음
for p = 1:P
if weighting_scheme == "tent"
top = top + weighting_tent(images(i, j, c, p))* linear_images(i, j, c, p)/EB(p);
bottom = bottom + weighting_tent(images(i, j, c, p));
else
top = top + weighting_uniform(images(i, j, c, p))* linear_images(i, j, c, p)/EB(p);
bottom = bottom + weighting_uniform(images(i, j, c, p));
end
end
HDR_images(i, j, c) = top/bottom;Logarithmic merging
Logarithmic merging에서는 앞서 구한 linear_image에 log를 씌웠음
for p = 1:P
if weighting_scheme == "tent"
top = top + weighting_tent(images(i, j, c, p))*(log(linear_images(i, j, c, p)) - B(p));
bottom = bottom + weighting_tent(images(i, j, c, p));
else
top = top + weighting_uniform(images(i, j, c, p))*(log(linear_images(i, j, c, p)) - B(p));
bottom = bottom + weighting_uniform(images(i, j, c, p));
end
end
HDR_images(i, j, c) = exp(top/bottom);Evaluation
앞서 구한 HDR 이미지들을 평가하기 위해서 이미지에 있는 color checker를 사용하여 밝기가 linear한지를 확인하였음. 먼저 color checker가 잘 보이는 이미지를 가지고 6개의 patch에 대한 좌표를 구하였음
imshow(images(:,:,:,15)/255);
R_list = cell(6, 1);
for i =1:6
[x, y] = ginput(2);
x = round(x); y = round(y);
R_list{i} = [x(1) y(1) x(2)-x(1) y(2)-y(1)];
end이후 HDR 이미지를 XYZ color space로 바꾸어 Y값을 추출하였음
XYZ = rgb2xyz(HDR_images, 'Colorspace', 'linear-rgb');
Y = XYZ(:,:,2);각각의 patch에 대하여 평균값을 구하고
average_luminance = zeros(2, 6);
for i =1:6
color_checker = imcrop(Y, R_list{i});
average_luminance(1, i) = i;
average_luminance(2, i) = log(mean(color_checker(:)));
end6개의 평균을 가지고 linear regression을 진행하였음
mdl = fitlm(average_luminance(1, :), average_luminance(2, :));
plot(mdl);이를 가지고 error sum을 구하였을때의 결과는 다음과 같음
몇개의 결과를 제외하고 대체적으로 비슷한 결과를 보였으나 육안으로 확인하였을때 Rendered logarithmic tent의 결과가 가장 만족스러웠음. 따라서 이후의 과정에서 Rendered logarithmic tent의 결과를 사용함.
Result
- Rendered linear tent: 0.1637
- Rendered logarithmic tent: 0.0026
- Rendered linear uniform: 0.0069
- Rendered logarithmic uniform: 0.0030
- Raw linear uniform: 0.0013
- Raw linear tent: 0.0024
- Raw logarithmic uniform: 0.0030
- Raw logarithmic tent:0.0890
2. Tonemapping
Photographic tonmapping
과제에서 주어진 tonemapping방식을 각각에 color channel에 관하여 별도로 적용했을때의 코드는 다음과 같음
K = 0.95;
B = 0.5; %burn
a = 0.01;
[W, H, C] = size(HDR_images);
N = W*H*C;
sum_=0;
for w = 1:W
for h = 1:H
for c = 1:C
sum_ = sum_ + log(HDR_images(w, h, c)+a);
end
end
end
I = exp(sum_/N);
tone_images = zeros(W, H, C);
for w = 1:W
for h = 1:H
for c = 1:C
tone_images(w, h, c) = K/I*HDR_images(w, h, c);
end
end
end
white = B*max(tone_images(:));
for w = 1:W
for h = 1:H
for c = 1:C
tmp = tone_images(w,h,c);
tone_images(w, h, c) = tmp*(1+(tmp/white^2))/(1+tmp);
end
end
end본 코드의 결과는 다음과 같음. 이미지의 밝은 부분과 어두운 부분이 모두 source image들에 비해서 뚜렷하게 보임. 하지만 밝은 부분의 경우 다소 뿌옇게 보임.

luninance channel Y에 대해서만 tonemapping을 적용할 경우 위와 비슷한 코드를 사용함. 앞뒤로 RGB 이미지를 XYZ 이미지로 변환한 후 xyY 이미지로 변환하고 다시 복구하는 작업이 추가되어있음. K = 2, B = 0.9를 사용함.
XYZ = rgb2xyz(HDR_images, 'Colorspace', 'linear-rgb');
cform = makecform('xyz2xyl');
XYZ = applycform(XYZ, cform);
...
cform = makecform('xyl2xyz');
XYZ = applycform(XYZ, cform);
rgb = xyz2rgb(XYZ, 'Colorspace', 'linear-rgb');앞선 이미지에 비해여 밝은 부분이 조금 더 뚜렷하게 보임. 하지만 이미지의 색감이 너무 노랗게 변하여서 좋은 결과라고 할 수 없음.
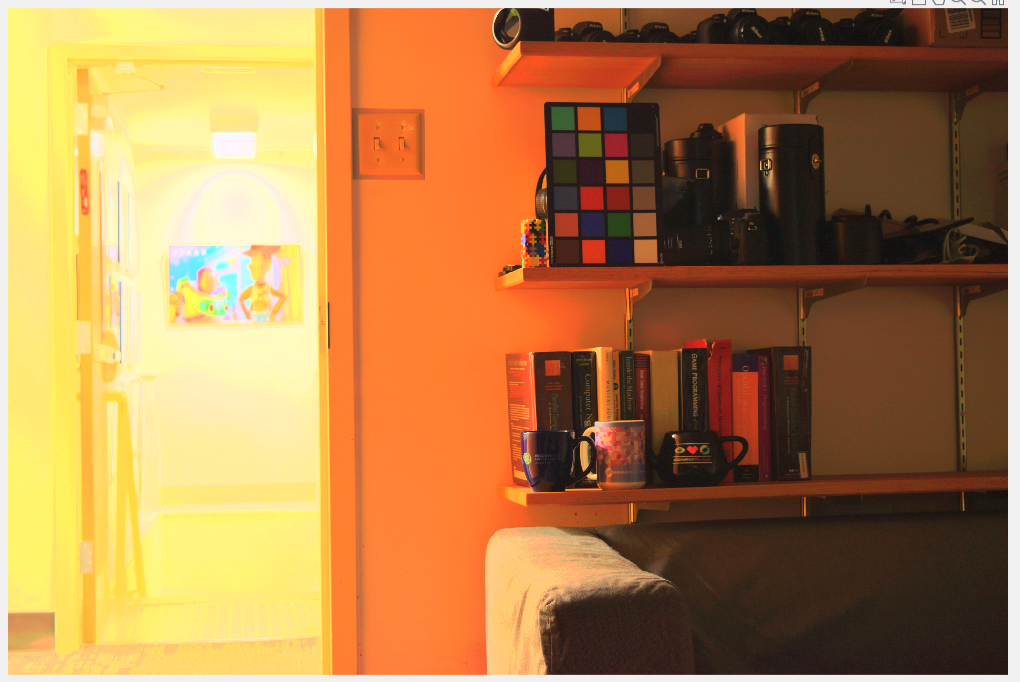
결과적으로 RGB 이미지로 진행한 결과가 더 마음에 듬.
Tonemapping using bilateral filtering
앞선 알고리즘과 마찬가지로 bilateral filter를 사용한 tonemapping도 RGB 이미지를 사용한 경우와 밝기값만을 사용한 경우 모두 진행하였음.
% 1. Compute the log intensitiy
L = log(HDR_images);
% 2. Compute the base layer using bilatering filtering
B = imbilatfilt(L);
% 3. Compute the detail layer
D = L - B;
% 4. Apply an offset and a scale S to the base
S = 0.15;
B = S * (B-max(B(:)));
% 5. Reconstruct the intensity
tonemapping_images = exp(B + D);이에 대한 결과는 다음과 같음. 앞선 결과들에 비해서 밝은 부분과 어두운 부분 모두 잘 보임. 하지만 이미지의 채도가 낮아진 것을 볼 수 있음.

이전 알고리즘과 마찬가지로 전체적인 구현을 비슷하나 앞뒤로 이미지의 color space를 RGB에서 xyY로 변환하는 과정이 붙음. S = 0.18를 사용하였음. 이에 대한 결과는 다음과 같음. 마찬가지로 어두운 부분과 밝은 부분의 결과가 매우 좋으나 색감이 매우 붉어졌음.

따라서 RGB 이미지로 진행한 결과가 더 마음에 듬.